W jaki sposób będą wybierani teraz posłowie na Sejm RP? Na podstawie stworzonej w 1878 roku metody Victora d’Hondta (1841-1901), belgijskiego prawnika i matematyka, profesora uniwersytetu w Gandawie. Opracowana przez niego XIX-wieczna metoda podziału mandatów parlamentarnych w wyborach proporcjonalnych wzbudza jednak od lat potężne kontrowersje w wielu kręgach społecznych.

Warto z pewnością uzmysłowić wszystkim zainteresowanym, że belgijska koncepcja matematyczna nie zawsze była wykorzystywana w wolnej Polsce, po historycznym przełomie ustrojowym sprzed 34 lat. W wyborach parlamentarnych w 1991 roku oraz w 2001 roku zastosowano w naszym kraju inne rozwiązanie.

Skorzystano wtedy z konkurencyjnej metody, której autorem był francuski matematyk André Sainte-Laguë (1882-1950). W pozostałych przypadkach stawiano jednak zwyczajowo na d’Hondta, bo belgijski wzorzec matematyczny cieszył się wśród polskich elit politycznych większym uznaniem, niż patent francuski, preferujący – w największym uproszczeniu – liczby nieparzyste.

Magia ilorazów

Nie jest łatwo wyjaśnić jasnym i przystępnym językiem, na czym w istocie polega metoda d’Hondta. Jako syn nauczyciela matematyki spróbuję wszakże podjąć się tego zadania. By to zrozumieć, trzeba tylko wiedzieć, co to jest iloraz, licznik, mianownik oraz liczba naturalna. Mam jednak nadzieję, że przytłaczająca większość czytelników zetknęła się w swoim życiu z tymi niezbyt skomplikowanymi terminami matematycznymi.

O wyborczym sukcesie przesądzają w oczywisty sposób tzw. ilorazy wyborcze. Licznikami w politycznych ułamkach są całkowite liczby głosów uzyskanych przez dane komitety wyborcze, a mianownikami – kolejne liczby naturalne (w ordynacji francuskiej – liczby nieparzyste). Należy je po prostu dzielić przez siebie. O podziale miejsc pomiędzy poszczególnymi komitetami wyborczymi decydują wielkości obliczonych w ten sposób ilorazów.

Są one ustawiane w szeregu, od największego do najmniejszego. Mandaty w Sejmie RP przydziela się zgodnie z wynikającą z obliczeń kolejnością, poczynając od najwyższego wyniku do najniższego, aż do momentu, w którym liczba dostępnych miejsc ulegnie wyczerpaniu. Procedura ta jest stosowana w każdym z poszczególnych okręgów wyborczych, a nie odgórnie w skali całego kraju.

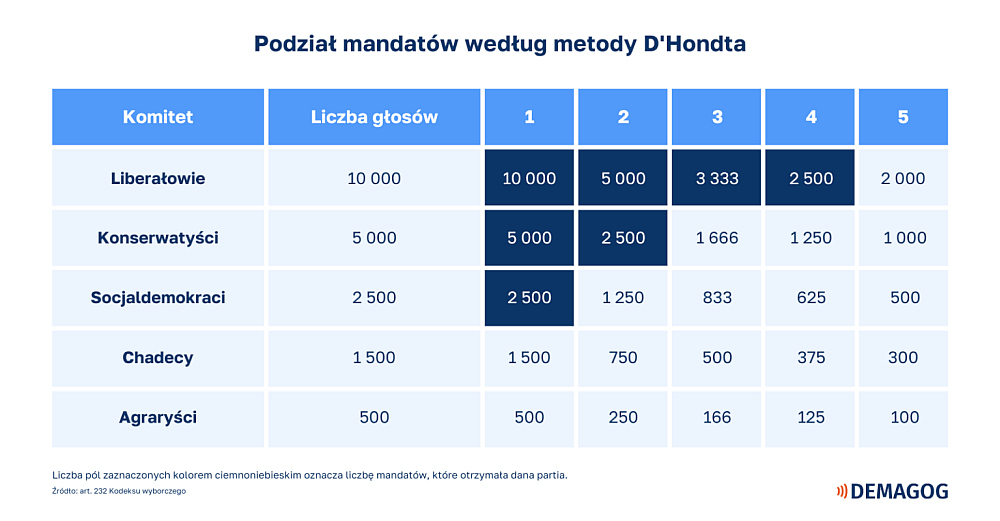
Poniższa tabela obrazuje na abstrakcyjnym przykładzie sposób przydzielania mandatów w danym okręgu wyborczym.

Nie tylko w Polsce

Proste? Nie tracę nadziei, że jest to zrozumiałe. Taki sposób wyłaniania posłów w wyborach proporcjonalnych stosuje się nie tylko w Polsce, ale i w innych demokratycznych krajach europejskich, w tym m.in. w Austrii, Finlandii, Holandii i Hiszpanii. Czy metoda d'Hondta rzeczywiście premiuje zwycięzcę, jak uporczywie twierdzą niektórzy?

Otóż nie. To stereotypowy mit, który od lat krąży w naszym kraju. Ugrupowanie, które nie zdobyło w wyborach największej liczby głosów, może uzyskać najwięcej mandatów w Sejmie, co wcale nie jest politycznym paradoksem. Największe partie polityczne promuje bowiem nie sama metoda d’Hondta, ale kombinacja belgijskiej receptury matematycznej i wielkości okręgów wyborczych. Im mniejsze okręgi, tym wyższy jest tzw. „próg naturalny”, czyli poziom poparcia społecznego, pozwalający się „załapać” określonej partii politycznej na mandat poselski w okręgu.

Konstytucyjne realia

Ordynacja proporcjonalna ma swoich zwolenników i zdeklarowanych przeciwników. Liczni politycy i komentatorzy głoszą od dawna tezę, że rzetelne i uczciwe byłyby tylko wybory większościowe w tzw. jednomandatowych okręgach wyborczych. Wymagałoby to jednak zmiany obowiązującej Konstytucji RP, której art. 96 wyraźnie stanowi, że wybory do Sejmu RP są „powszechne, równe, bezpośrednie i proporcjonalne”. Matematyka, która jest niewątpliwą królową nauk, zależy więc również od polityki, choć może się to na pierwszy rzut oka wydawać absurdalne.

Jedyne, co można robić w istniejących realiach konstytucyjnych, to ustanawianie różnych procedur wyłaniania posłów. Raz może to być metoda belgijska, a innym razem - francuska. Byleby odpowiadała wymogom wyborów proporcjonalnych…